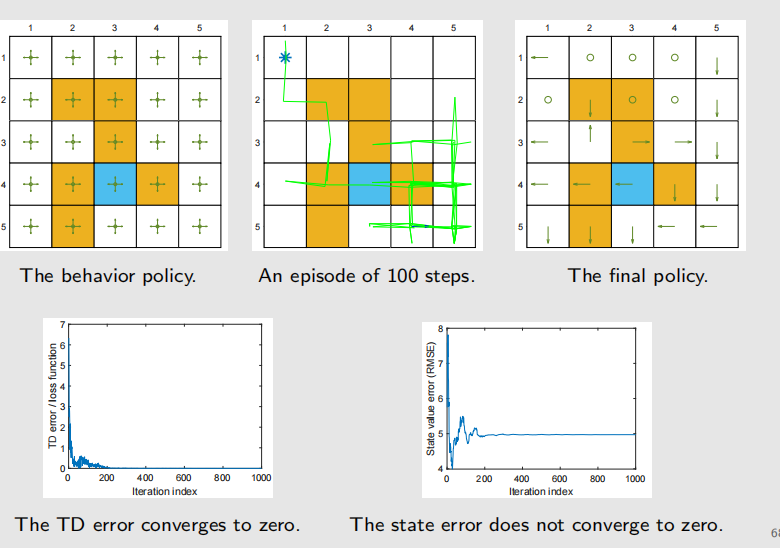
之前我们介绍的是基于表格的方式,现在我们要介绍基于函数的方式。现在开始,我们要引入神经网络。此外,现在讲的都是基于值的,下次将介绍基于策略的。
虽然我们没有明说,但我们目前为止确实是以表格方式存储数据的,比如:
显然当state
space连续或者巨大无比的时候,这种方式就不能用了;同时泛化能力也不能得到保证。引入函数近似的话,这些问题就可以解决了。假如我们有好多好多状态s,每个都对应一个v,那能不能用一条曲线来拟合v-s关系呢?
最简单的就是直线,可以写成: 当然了不用想都知道这是不准确的。我们也可以用高阶曲线去近似:
或者用神经网络去模拟。模拟的好处是,可以用比state
space的大小更少的参数去存储,并且具有很好的泛化性(就是如果改变一些state
value,可能相邻的state
value也会改变,而不需要访问所有的state)。下面是正式的介绍。
state value estimation
这节都讲的是重要的方法。
objective function
我们的目的是找到最优的去让我们的去最好的近似我们的。这实际就是在policy
evaluation。为了找到最优的,我们就要找到定义目标函数,并且去优化。
目标函数的定义为:
这里的S是个随机变量,它的概率分布是什么呢?第一种方式是把所有S看作是平等的,这样目标函数就是:
但是这里有一个问题,因为目标状态和它相邻状态可能是更重要的,重要的状态应该有更大的权重,这样它们估计的误差就比较小。因此我们引入第二个概率分布:stationary
distribution(平稳分布,可能是这么翻译的吧),它表述了一个马尔科夫过程的long-run
behavior。
我们用描述这个分布。因此我们有。这样,目标函数就可以写成:
所谓平稳,就是从现在出发,执行某个策略跑了很多很多步后,达到的一种概率分布,这时候是达到平稳的状态了。这个分布在值函数近似和策略梯度中都很重要。
例如,假设我们有如下探索性策略:
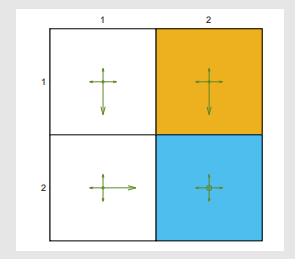
那么我们可以定义: 如果我们执行很多很多步,做一个long
run,那么这个概率分布最后就会趋向于如图所示:
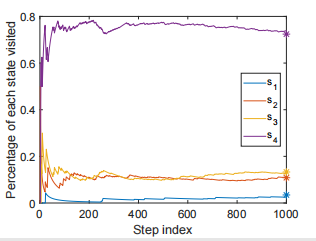
我们注意,上图的后边末端有星号标注,这些是理论值。实际上,我们不需要跑很多次也能找到这个理论值,这个值怎么找呢?我们有这样的式子被满足:
这个式子其实就是说明到平稳态了。其中,是我们的状态转移矩阵,
每一个元素代表了s到s'的概率。显然,是对应特征值为1的特征向量(这里注一下,我认为应该是P转置的特征向量),在本例中状态转移矩阵为:
那么可以求出:
优化算法
我们要优化这个目标函数。一般方法会想到梯度下降,那我们就求一下梯度:
但是我们这里要计算一个期望,怎么去避免?我们很自然想到stochastic
gradient来避免求期望,因此就有更新公式: 学习率后面那一坨把原先的梯度近似替代的东西。其中,是对S的采样,被合并成了以保持简洁。但是呢,我们这里涉及了,但是我们是要求它,我们是不知道的,所以我们要用其他量代替它。代替的方法有两种:
第一种便是MC方法:就是把从出发的episode的discounted
return,即,近似当做。第二种是TD方法:就是用(也就是TD
target)去代替。由此得到以下算法伪代码:

这里我们提到了linear case。这是特定的对的选择,虽然我们到现在还没讨论怎么选择它;我们可以选择线性的或者非线性的。
近似函数选择
怎么选取?有两种方法,一是用线性模型,之前我们介绍过;二是现在广泛使用的,就是用神经网络去逼近这样一个函数,输入一个s就能输出一个。
如果是线性的,那么梯度就是:
这就得到了我们刚刚展示给各位的伪代码中的公式(就不再复制过来了)。这种方式叫做TD-Linear。这种方式的缺点就是feature
vectors太难选了,这也是为什么它逐渐被神经网络替代。当然它也有好处,第一是理论性更好去分析(神经网络的理论性很难分析);第二就是表征能力还是有的,而且tabular
representation就是linear function
approximation的一个特殊情况(就是把看作是第s个元素为1而其他都是0的列向量)。
举例
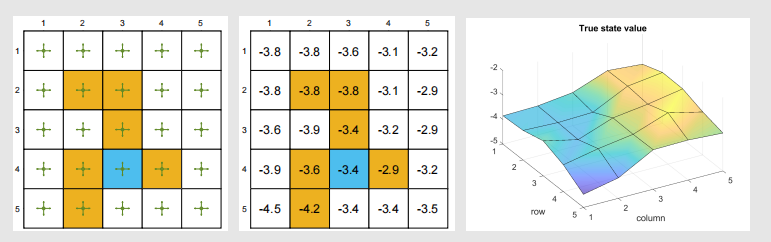
先给出我们的例子、真实的状态值和曲线表示:
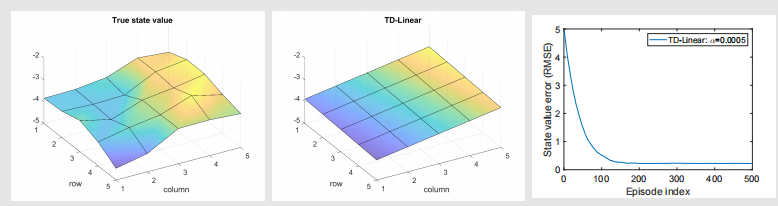
假设我们根据策略得到了500个episodes,每个episode有500steps。每一个episode的初始s,a是均匀随机的。使用TD-Linear,我们拟合曲面,选择如下特征向量:
由此得到: 这个显然是三维空间的一个平面。最后得到的结果如图:
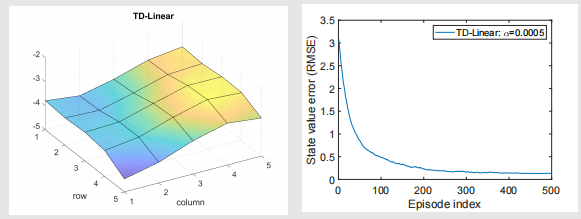
可以看出虽然最后收敛了,但是误差也不是零。如果想更好的拟合,就要用更复杂的高阶曲面,需要更多的参数,比如,我们选择如下特征向量:
当然我们还可以继续往上叠次方: 在三次方的情况下,最后结果如图:
值函数近似下的Sarsa和Q-leraning
在值函数近似下,Sarsa算法公式为: 其实就是v换成q了, 。这个算法还是在policy
evaluation,我们需要和policy improvement结合,就有了如下伪代码:

和Q-learning结合也差不多,它的公式就是: 区别就在于加了max,并且把max里面变成了。它的一个on-policy版本的伪代码为:

DQN
Deep Q-learning ,也叫deep
Q-network,是最早成功引入神经网络到RL的技术。神经网络在这里扮演的角色就是一个非线性函数:有一组参数w,输入s和a,输出。DQN要优化的目标函数(亦或者说损失函数)是:
括号里的东西其实就是Q-learning的TD-target,对应了bellman
optimal error,这是因为:
优化的方式是梯度下降。问题在于,如何计算梯度?这也是DQN的一个重点贡献。我们要求对w的梯度,但是J(w)里有两个含w的式子。后面含w的那一项好算,但是前面那一项不好算(因为他是max函数,这是不可导的!但是N那种ReLU、maxpooling又怎么反向传播呢?可以看看这个:relupooling_argmax
求导_Jumi爱笑笑的博客-CSDN博客)。在DQN中,它把前面整个假设为了y:
假设y里面的w是一个常数,这样J(w)就相当于只对后面的w求梯度了。为了实现,DQN引入了两个网络:一个是主网络,用来代表;另一个是目标网络(target
network),为。主网络的w一直随着新采样进来而更新;而target
work并不是在一直更新,而是每过一段时间就把主网络的w给赋值过来。此时目标函数就变成了:
这样优化的时候,先假设不动,然后计算对w的梯度,然后再去优化J。这样w和都能收敛到最优值。这样一来,J的梯度就是:
Experience replay
经验回放,RL专有名词,是DQN里出来的技巧。我们收集数据(即experience)时是有先后顺序的,但是用的时候不是谁先来就用谁。我们把他们数据储存到一个集合,定义为:。这个集合就叫replay
buffer。每次训练神经网络时,就从这个集合里拿出一些samples,拿出来用的过程就叫experience
replay;拿出来的过程应该均匀分布,保证每个数据拿出来的概率相同。
我们为什么必须要用经验回放?为什么要均匀分布?关键就在与我们刚刚讲的目标函数J。我们的随机变量有R,S',S,A;我们把(S,A)看成一个随机变量(的索引),服从分布d,之后再说。R和S'服从于系统的模型,,不作过多讨论。回到(S,A),我们假设它们是均匀分布的。我们没有先验知识,所以不能看作高斯分布什么的,只能一视同仁。
好了,现在我们要求它们均匀分布,但我们采集数据是按其他分布采集的,所以我们就要把数据放在一起打散,然后均匀采样,这样就打破了不同sample之间的correlation。为什么基于表格的算法就不要经验回放,换言之,不需要(S,A)均匀分布?因为DQN是在做一个值函数近似,在对一个标量目标函数做优化,涉及到(S,A)的期望,这就涉及到(S,A)的分布。而基于表格的方法是在求解BOE,这个期望和(S,A)无关,它们是内部的概率模型。
再者,经验回放可以让样本更有效的被利用,因为会被重复利用。在确定性环境中(随机性不谈),我们只要保证所有(S,A)
pair都被访问到,丢到经验缓冲池里用就行了,而不需要访问庞大的步数作为一个episode。
实现
DQN的off-policy伪代码如下。

其实这是简化版的,原文还用了更多的技巧,用了更高效的神经网络。看看这个max:在我们的例子中,我们输入s和a,神经网络只会输出一个q,这样我们每个s有五个a,我们求解就要经过五次神经网络;而原论文的神经网络时直接输出一堆q,然后这样max就显而易见了。
不过捏显然DQN对于数据要求是很高的。加入数据不好,就会变成下面这样: