策略梯度方法和下一节的AC方法是现在越来越流行的方法。之前所有的方法都是value-based,现在开始的方法都是policy-based的。而基于策略的方法呢,是直接建立一个策略相关的目标函数(从value
function 到 policy
function),直接优化这个函数就会得到最优策略。而AC方法则是结合了基于策略和基于值的方法。
基本思想
目前为止,我们所有的策略都是表格表示的,如图所示:
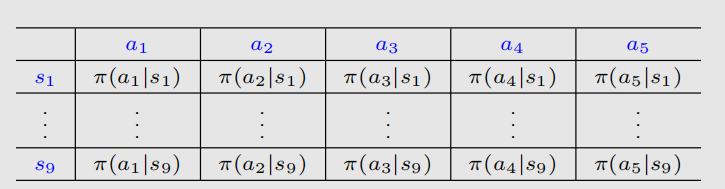
下面我们把表格改成函数,关于策略的写法也会改变: 这个是一个向量,表示π这个函数里面的参数。现在用的最广泛的函数形式便是神经网络,输入s后,经过参数(策略函数是,值函数是w),得到一组对应不同action的π。优点与之前讲值函数是一样的。
用表格表示的时候,我们说策略π是最优的,如果它能让每个状态价值最大;那如果用函数表示,该怎么定义最优策略?我们定义如果π最优,那么它就最大化了一个scalar
metric,这个metric也在这里称为我们的目标函数。我们定义目标函数为。那么我们希望的即为。最简单的优化算法就是:
别忘了我们是最大化而不是最小化。现在问题是,怎么取目标函数?怎么去求解对应梯度?这些还是有复杂的东西在里面的。
目标函数
average value
我们如何选择metric(即目标函数,我也不知道为什么叫法不一样)?在这里,我们会经常遇到两大类metric。
第一大类叫average state value,或简称average
value。这就是对state value的一个加权平均,这个metric被定义为:
d(s)是权重,和为1且都为正。这个呢就是个策略的函数,不同的策略对应的值也不同。当然,把d看成一个分布的话,也可以写成:
两个式子是一样的。当然了,也可以写成向量形式:
这样的形式有助于我们分析。那么我们怎么去选择分布d呢?第一种情况就是d是独立于策略π的,这样我们求梯度的时候就只需要求的梯度。这种情况下,我们就把d和写成和。最简单的情况就是均匀分布:=1/|S|;或者,我们关心一些特殊的状态,比如作为我们游戏开始的状态。极端情况是我们只关心这个状态,这样就变成了。
第二种情况就是d和π有关系。这种方式很常见:我们选定d为基于π的平稳分布(之前讲过),即。正如上节所说,只要知道,就能知道这个平稳分布(当然也可能不知道P,不展开细说了..)。反正,访问多的状态权重应该多一些,反之则少。
实际上,我们如果读论文的话,我们还会见到的另一种写法: 证明的公式为:
Average reward
第二种目标哈数就是average one-step
reward,简称averagereward。它的函数被定义为: 这里, 这里的权重d是依赖于策略π的,是stationary
distribution。这里的r(s,a)也是一个均值含义上的immediate
reward,它可以写作:
现在我们给出第二种等效的形式,在我们看论文看书的时候会经常遇到。假设我们现在有个策略,依据这个策略形成了一个trajectory,得到了很多reward:;我们把这些reward加起来求个期望再求个平均,得到如下式子:
它代表了跑无穷多步时reward的平均是什么、跑了无穷多步后,我们的就没用了,所以这个式子也可以写为:
这玩意就是我们刚才说过的。主要我们这里是immediate
reward,对于discounted case和undiscounted case都是成立的。
分析
直观上,由于用了return而用了immediate
reward,后者似乎要更short-sighted。然而实际上,两个metric是等价的。实际上我们可以证明:
证明略。这就说明,一方达到最优,那么另一方也就达到了最优。
梯度计算
计算梯度是整个策略梯度方法中最复杂的一部分。一是因为我们有很多不同的metric,二是因为我们要区分discounted和undiscounted的情况。但无论如何,这些梯度的结果都可以总结为这样的公式:
这里的等号可以是严格等于或者约等于或者成比例等于。在不同情况下对不同目标函数呈现出不同的分布。绝大情况认识这个式子就够了,除非是要科研创新。我们给出一些具体的例子:
我们又知道和是有关系的,因此我们有:
详细细节就不介绍了。现在我们对这些梯度作进一步分析。最重要的性质就是,梯度可以把所有的求和符合去掉,写成如下期望的形式:
这里的(S,A)是随机变量,S满足分布。先不说推导,为什么我们需要这样的式子?类似SGD,因为我们可以用采样的方式近似这个期望。这样,我们就可以用SGD来优化:
下面我们来看一下怎么得到这个公式。考虑我们出现的lnπ,这样就方便我们求导了:
这样我们变个型,就有了: 我们把这个式子代入梯度的表达式里,就可以得到期望的形式了:
这里的就是说S满足d的分布。现在我们还要做一些补充说明。首先,不同于之前,lnπ必须要让π大于0;因此我们引入softmax
function,把这些π归一化到(0,1)区间。学过ML的读者对此应该不会陌生。具体来讲,就是采用以下公式:
这里的h是另一个函数,类似于我们之前介绍value function
approximation里的feature
funtion。当然了现在基本都用神经网络了,输出层接个softmax就行了。由于我们的每个π都是大于0的,所以我们的策略是stochastic的,有探索性。但是如果action有无穷多个呢?那这种方法就不行了;但是接下来讲的deterministic
policy gradient是可以的。
梯度上升与REINFORCE
梯度上升的基本思路是:
实际上这是不能用的,因为有个期望,我们因为不知道环境模型,所以分布不知道,算不了期望,因此我们用随机梯度代替,就得到了:
但是这个式子也用不了,因为有个真实的action value:,我们不知道它。所以我们用某种方法近似它,用代替。第一种近似方法就是蒙特卡洛法,从(s,a)出发得到一个return,来近似代替。这种结合出来的方法就叫做REINFORCE。除此之外我们还可以用TD方法等等,这就引出了actor-critic,将在下一节介绍。
通常而言策略梯度是on-policy的,但是也有off-policy的,但是需要引入额外技巧,在下一节说明。下面我们再重新组织一下这个算法。由于:
因此算法可以重写成: 这样我们就得到了算法的一种重要表达形式: 可以看出这是一个优化的算法,步长是。从微分的角度,我们有:
这是微分意义上的。如果差太多,这种近似就不精确了。
当我们把原先梯度上升公式的代入,就得到了:
向量的模长肯定是大于等于0的,所以我们可以知道:当时,选择的概率会增大,因为,反之就是变小。
能够很好的平衡exploration和exploitation。为什么这么说?从的定义可以看出,它与分子成正比,当q比较大β也会比较大,这就意味着π值会被增大;这就意味着如果action
value大,就会有更大的概率去选它,这就是exploitation。可是,β又与分母的π成反比,当π值比较小,β就会比较大,就会让π值变大,这说明如果我选择的概率比较小,那下个时刻我会更大概率去选它,这是exploration。
现在来看具体算法。记住我们现在的公式变成了: 这里用的是。如果我们用MC方法去估计它,那么这个算法的具体名字叫做REINFORCE,它是最早的最简单的策略梯度算法。REINFORCE的伪代码为:

注意我们的MC是off
line的,我们必须把所有episode全采集完后开始跑,不能边更新边采集。之后介绍基于TD的方法后,就可以变成on
line的了。



