在本篇中,围绕 optimal state value(最优状态价值)和optimal
policy(最优策略),我们需要贝尔曼最优方程( Bellman optimality
equation,BOE)来解决。强化学习的目的便是寻找最优策略。问题的背景是,如果我们的策略不够好,该如何去改善它?以上一章最后的图例为例:
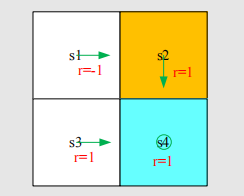
求解每个状态价值的过程就省略了。可以得到s1的每个action
value为(给定衰减系数为0.9): 显然我们采取a2是不够好的,从上面可以看出我们应该选择a3.
那么,现在我们的s1处的策略就可以写成: 其中:,也就是action
value最大的action。注意到我们这个例子比较简单,是因为除了s1,别的状态的策略都已经是最优的了。那如果别的状态的策略都不是最优的呢?那此时我们计算s1的value最大的action,那就不一定是最好的action。事实上,我们可以不断迭代这个过程。这个过程就需要我们的贝尔曼最优公式了。
Definition:定义
首先是关于optimal
policy的定义。这个定义非常简单,我们定义:一个策略是最优的,如果对于所有的s和任何其他的来说,都有。这个定义引出一些问题: 1.最优策略一定存在吗?
2.最优策略唯一吗? 3.最优策略是确定性的吗(deterministic)?
4.如何得到最优策略? 当我们研究完了BOE,这些问题可以悉数回答。
下面是BOE的定义,他只需要在贝尔曼公式的基础上做一点改动(加一个max):
在这个公式中,都是已知的,都是要计算的。同时,不同于贝尔曼公式,BOE中的也是不知道的,是我们要寻找的。把这个式子写成向量形式,就是:
这里的是指对向量每个元素取最大值。这是一个类似x=f(x)的式子,对此我们有专门的求解方法,之后会介绍。
利用收缩映射定理求解BOE
在介绍收缩映射定理之前,我们先考察待优化等式:的右侧。我们可以先考察一个看起来比较简单的式子:给定q1,q2,q3,求解:
那显然呢,如果我们假设q3是最大的,那么如果要让这个式子最大,就要尽可能让q3的权重c3最大,因此,且最大值就是。同样的,对于我们的贝尔曼公式,就显然有:
其中当:
时得到最优值。当然了,这只是对一个状态而言,我们最终是对所有状态求解的。我们令:
这样BOE就变成了 的形式。其中,f(v)向量的代表状态s的元素为:
那么我们如何求解这个类似于的式子呢?我们需要用到Contraction
mapping
theorem,即收缩映射定理。具体的数学上的证明过程就不介绍了。
为介绍这个定理,首先介绍一个概念:fixed
point,即不动点。设f是空间X到X的映射,x属于X,那么当f(x)=x时,称x是一个不动点。
之后需要介绍另一个概念:Contraction
mapping(收缩映射)。我们称f是一个收缩映射,如果:
现在,就可以隆重介绍我们的收缩映射定理了:对于任意形如的方程,如果是一个收缩映射,那么:
1.必定有且仅有唯一的一个,使得;
2.考虑一个序列,其中,那么当时,。这意味着我们可以迭代地求解出这个值(初值自己定),且这个收敛速度是很快的(指数级别)。
一个简单的例子为:

知道了这个定理,我们就可以把它应用到BOE里。我们知道BOE为: 对于这个式子,我们有。其中就是衰减系数。对于这个我们就不做证明了,总之我们可以知道是一个收缩映射(也可以叫收缩函数),因而我们知道,总是存在一个唯一解,并且可迭代地求解:
这个收敛很快,收敛速度取决于衰减系数。这个形式是向量形式的,是对所有state而言的,对于每一个state而言就写成如下elementwise
form: 到此我们说完了BOE的求解,总结一下它的流程如下:

这个算法就是值迭代算法,之后会提及。
求解举例
以下图为例:
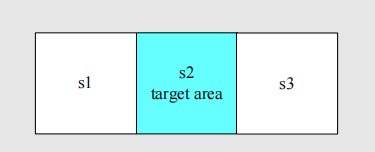
一共三个state,进入target的reward为1,撞墙是-1,进入普通状态是0。给定衰减系数是0.9。对于求解,**我们首先要刻画出一个q-value table**:
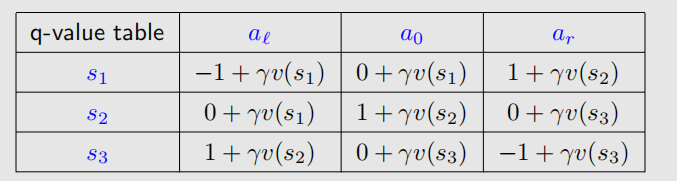
这样,我们就可以直接根据表内公式迭代,也算的很方便。
对于k=0时刻,我们设定三个状态的value都是0,那么表格此时就是:
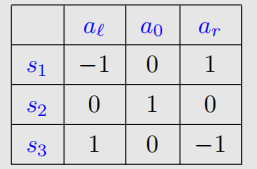
此时呢我们选择q值最大的策略,显然是: 那么对应的,各v值就是:v1=v2=v3=1.
k=1时刻,根据已有的v值更新q值表:
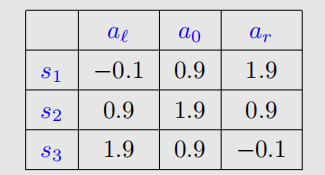
依旧可以得到:
并且此时的v值均为1.9,。当然我们不能无穷迭代下去,我们设定:如果两次v值的差在一个阈值内,我们就停止迭代。
BOE的最优性
我们已经迭代地找出了近似的最优解.那么假如我们知道了BOE的最优解,我们给定: 那么就得到了一个贝尔曼方程:
我们知道贝尔曼方程就是描述了给定策略下的关于状态的方程,那么这里得到的是否是最优策略呢?因为我们解BOE得到的是v值的近似最优解,而不是对求解。实际上确实如此,最优的v对应的就是最优的π,即:。这里就不给出证明了。
分析最优策略
我们的BOE长这样: 可见有三个关键因素是我们需要设计的:1.奖励设计:r
2.系统模型:两个p 3.衰减因子:。系统模型不是我们可以轻易更改的,我们可以更改的是r和。
首先关注。这个不用过多介绍,无非是衰减系数太大、太小、取中间值三种情况。太大,智能体会关注更长远的利益;太小,智能体会更关注眼前利益;如果为零,智能体甚至无法达到终点。就比如我们的grid
world,如果把衰减系数变得很大,智能体看的更长远,有时候就会进入forbidden;如果衰减系数变成0,就可能到不了终点,如下:
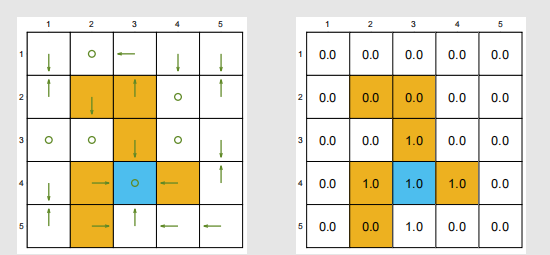
然后是r。在我们的grid world中,如果把进入forbidden
得到的reward变得很小(比如-1改成-10),那么智能体也几乎不会进入forbidden;那如果把每个r都改成ar+b呢?比如原先进入target是1,进入forbidden和边界是-1,其他情况是0;现在给这些r分别加1,变成2,0,1。答案是最优策略不会改变。也就是说,影响因素是奖励之间的相对值,而不是绝对值。
实际上呢,此时的各v值就变成了一个原v值的仿射变换:









