强化学习(四):值迭代与策略迭代
上一章的末尾我们提到了value iteration。这一章我们介绍value iteration和policy iteration——这二者都是截断策略迭代(Truncated policy iteration)的两个极端情况。
值迭代
值迭代分两步:
·1.policy update(PU)。
这一步求解当给出
·2.value update(VU)。
这一步求解
以上都是向量形式,为了给出具体算法,我们要将向量形式改写成元素形式(前者更适合理论分析)。伪代码如下。

策略迭代
不同于值迭代,策略迭代是先给出个初始策略
·1.policy evaluation(PE)。
这一步是计算贝尔曼方程的v。计算的方法是迭代方法,我们之前已经谈过了。
·2.policy improvement(PI)
根据step1算出的v,我们就可以得出每个状态的各个q值,进而更新greedy policy。
策略迭代的流程为:

截断策略迭代
我们刚才讲的两个iteration是很相似的:

考虑求解

截断策略迭代会导致最后结果不收敛吗?实际是不会的,因为
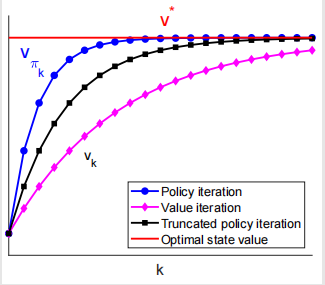
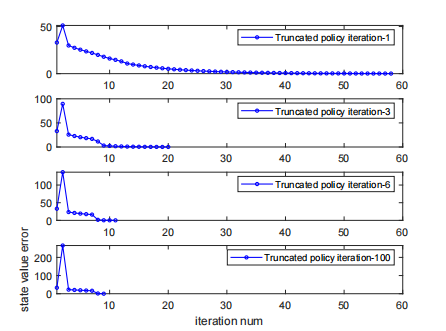
对于截断策略迭代来说,截断的迭代次数越大,收敛就越快;但是太大了也不行,计算代价会很高。这是一个关于截断位置的曲线的比较: