在此后的学习都是model-free的。为了之后Temporal-difference
learning(时间差分学习),需要先介绍本章知识。
上一节我们说过强化学习的一个核心词叫expectation,我们要去做mean
estimation,这也是蒙特卡洛的核心思想:我们用足够多的样本的均值去近似expectation。如何计算均值?如果要一次性计算,就需要等到所有数据收集后再算;另一种方法是增量地去计算,就是用一种递推的思想。我们令:
那么有: 因此我们得到了一个递推的公式: 如果把这里的1/k换成 ,
如果其满足一些条件,那么结果同样收敛到E(X)。这个估计均值的算法就是一种特殊的SA(stochastic
approximation)算法,也是一个特别的SGD(随机梯度下降)算法。
Robbins-Monro algorithm
这是SA中一个经典算法。SA代表了一大类算法,即stochastic iterative
algorithm,用于方程求解或者优化。它的特点是不需要知道方程的表达式从而求解。Robbins-Monro算法即RM算法是SA一个开创性工作,SGD便是RM一种特殊情况,前面的mean
estimation也是一种特殊的RM。RM算法是什么算法?考虑以下问题:我们现在有一个方程:
为了简化问题,我们的变量和函数都是标量意义的。这样的例子广泛存在,比如我们有一个优化问题,要优化这一目标函数,一般而言都是让其梯度为0,即如下方程:
亦或者,诸如的形式也可以。那么在不知道表达式的情况下,如何计算的根呢?下面正式介绍RM算法。RM算法是迭代的算法,形式如下:
其中是对根的第k次估计,)是第k次的对于g的带有噪音的观测(当然这个噪音也是不知道的,就是我输入w,输出的是噪声干扰后的g),是一个正参数(不一定是常量,比如可以是1/k)。
RM算法为什么会收敛?我们先举个例子:。我们给定:,那么最后的结果为:
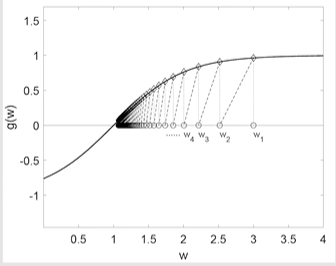
可以看出:越来越接近真实的解,且总是比更接近于解。至于严格的证明,下面会介绍,可以不看(
我们先给出RM定理:

然后是介绍。首先有个词叫with probability
1,简称w.p.1,是一个时常会在RL论文中证明时出现的词,因为是在不断采样的,不是常规意义的收敛,是概率上的收敛。三个条件中,第一个条件是关于g的梯度要求,第二个条件是关于系数的要求,第三个条件是关于测量误差的要求。下面解读这三个条件。
条件1:表明了g是递增的(递减的不行),保证了g(w)=0的根唯一存在。这个条件可以接受,因为大部分情况我们的g(w)是上述的J(w)的梯度,而g(w)再求梯度不就是J(w)的海森矩阵吗?海森矩阵正定,那么J就是凸函数;而我们大多情况也确实再进行凸优化。
条件2:后者的小于无穷保证了最后收敛到0;前者的等于0保证了不会收敛得太快。常见的就是1/k;但是这样的话在后期改变的幅度就会非常小了,所以实际中也会采用一个非常小的常数。
条件3:这是说的mean应该为0而variance有界。常见的例子就是是iid的,从一个常见的分布中采样得到(并不要求一定是高斯噪音)。
RM算法是如何应用到我们的均值估计的呢?回想均值估计公式: 如果,那么。我们考虑函数:。我们要求解g(w)=0的根,这样就能求出E(X)。但是我们不知道大E(X),因此我们对X进行采样,所以我们测量的即我们的observation就是。进一步,就可以写成: 那么对应的RM算法公式就是: 这个就是我们的mean estimation
algorithm。实际上有一个比RM定理更普适的定理:

该定理的扩展可以用于后面的Q-learning和TD算法。
SGD
stochastic gradient
descent,即随机梯度下降,是ML中大家肯定会接触的一个概念。SGD可以看作是RM的特殊情况。由于是ML中比较基础的东西这里就不详细阐述了。假设我们有如下待优化函数:
我们有很多方法求解,我们依次递进的给出三种方法。方法一就是普通的梯度下降,即GD:
GD的缺点是期望值比较难获得(或者求解需要大量计算)。方法二是batch
gradient descent即BGD:
就是用所有采样的样本的均值去近似期望。方法三就是SGD:
就是BGD的n=1的特例。当距离很远时,SGD与GD效果差不多;反之,SGD会在距离进的时候体现随机性。证明用到拉格朗日中值定理,这里就不赘述了。当然还有介于BGD和SGD之间的MBGD,即mini-batch
GD。




