强化学习(一):基本概念
从本文开始,均是针对哔哩哔哩网课的笔记记录。本文参考:【强化学习的数学原理】课程:从零开始到透彻理解(完结)_哔哩哔哩_bilibili
本文是对基本概念的介绍。
笔记背景范例
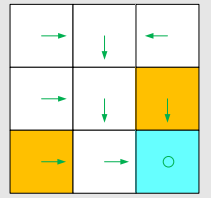
本课程的背景例子如图:
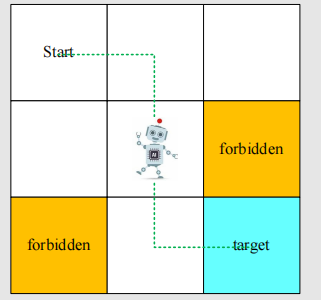
这是一个网格世界,我们的机器人要从给定的起点出发,寻找一个合适的路径到达我们的目的地(也就是我们的task)。机器人只能向相邻四个方格移动,且整个网格世界存在边界。我们的机器人要尽可能避免进入forbidden,且不能超越边界。 以此背景,我们介绍下面概念。
State:状态
state是指智能体相对于环境所处的状态。在我们的例子中,不同的方格代表了不同的状态,是一个包含x,y二维坐标信息的向量。如图所示:
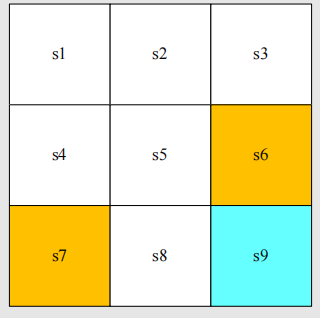
state space:即状态空间,也就是所有状态的集合:
Action:行动
action是指对于每一个状态,智能体拥有的一系列可以采取的行动。对我们的例子来说,共有如下五个状态:
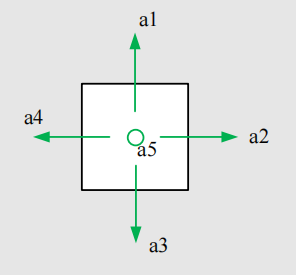
a1~a5依次是向上、向右、向下、向左已经保持不动。
Action space of a state:
某个状态的动作空间。需要注意,不同的状态,动作空间可能是不一样的。公式表示为:
State transition:状态迁移
当采取一个action时,智能体可能会从一个state变到另一个state,这就叫做state transition。它实际上是定义智能体和环境交互的一种行为,我们可以(在本例子的游戏环境中)任意定义这一行为。
比如说,我们在s1状态采取行动a1,也就是撞到边界,我们可以定义智能体保持不动:
又或者,当我们撞到forbidden area时,我们有两种方案:要么进不去原地不动,要么能进去但是会受到惩罚(penalty)。普适地,我们选择后者方案,因为agent冒险进入forbidden area的话或许会能得到更好的通往target的路径。
我们可以得到如下table:
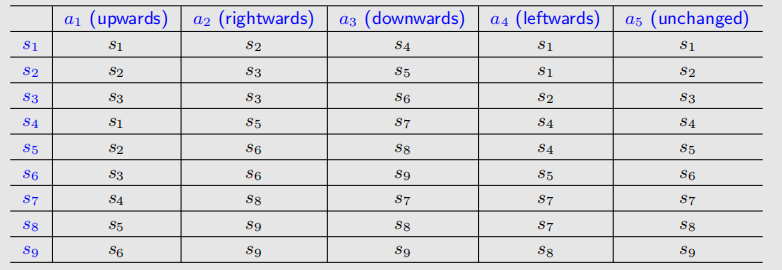
但是,通过这张表无法表达转换成多个状态的可能性。因此,我们采用State
transition
probability来从数学上表述;对于这种确定性案例(deterministic
case),我们用数学语言表述为:
Policy:策略
policy是强化学习独有的概念,它用来告诉智能体在当前状态该采取什么行动。如图,这些箭头就表示了一个策略:
当然,我们需要一种更数学的方法去表示。在强化学习中,我们使用条件概率,用
我们可以用一张表来描述policy:
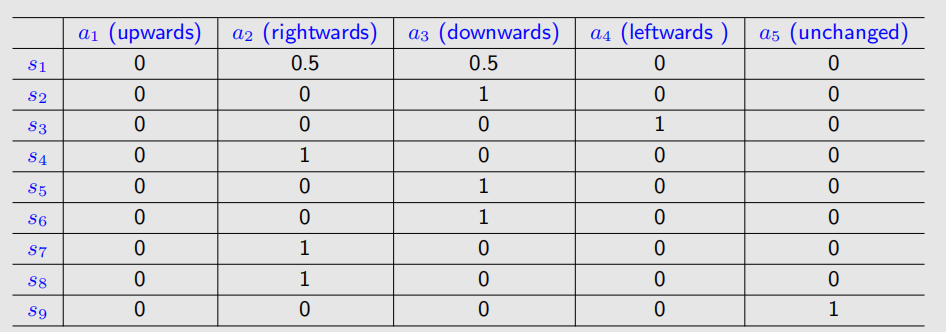
注意到,这张表可以即表示deterministic,又表示stochastic,而不同于上面的状态迁移表只能表示deterministic。实际编程中,我们可以用数组或矩阵表示这样一个策略。
Reward & Return:奖励 & 累积回报
Reward是RL中独有的概念,是指采取一个行动后智能体得到的一个实数,一个标量。正值表示鼓励这样的行为,负值表示作出惩罚。正值也可以表示punishment。
在我们的范例中,我们可以如下设计reward:
1.智能体尝试越出边界,则
2.智能体尝试进入forbidden,则
3.智能体到达target,则
4.otherwise ,
我们同样可以用一张表格描述reward:
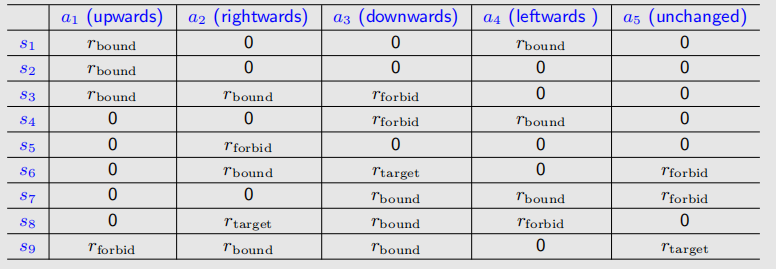
但是这种只能表示deterministic
cases,我们依旧使用条件概率来表示stochastic
cases。比如,如果我们努力学习,我们就会获得reward,但是我们得到多少是不确定的:
一个trajectory是一个状态-行为-奖励链,比如:
这样的话会有一个问题:加入我们的trajectory是无限的,它在target处一直原地转圈,如下:
Episode:回合/轮次
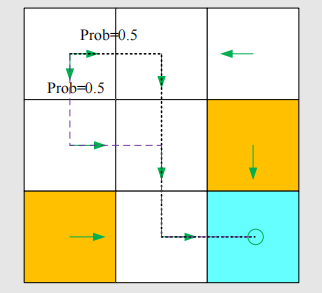
当我们遵循一个policy与environment交互时,智能体可能在一些终止状态(terminal states)停下来。由此得到的trajectory被称为一个episode(也可以叫一个trial)。可以说一个episode可以被描述为一个有穷的trajectory。如图便是一个episode。
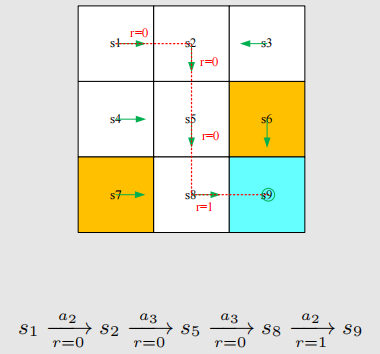
然而有些任务是没有terminal states的。这意味着我们与环境的交互无法终止。这样的任务叫做continuing tasks。事实上,我们可以用一个统一的数学方式,把episodic tasks转化为continuing tasks。以本案例为例,我们有两种做法:
1.把target state看成一个特殊的absorbing state,只要智能体进入这个state,就永远不会离开,之后reward都是0.
2.把target state看成一个普通的state。智能体可以选择离开,也可以在再次进入后获得+1的reward。
本案例中我们选择第二个方法,这就就可以方便把target state看成一个normal state。
Markov decision process(MDP):马尔科夫决策过程
几乎所有强化学习问题都可以转化为MDP,它是强化学习问题的理论基础。马尔科夫是一个无记忆的随机过程,可以用一个元组
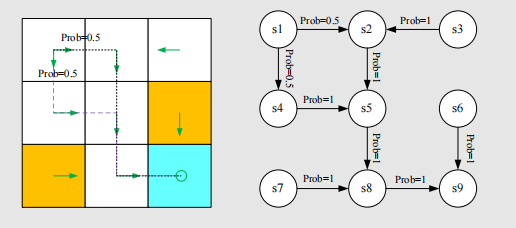
具体来说,MDP包括以下关键元素。
· Sets(集合):
- State:状态集合
- Action:行动集合
- Reward: 奖励集合
· Probability distribution(概率分布):
- state transition probability:
- reward probability:
· Policy:
· Markov property:无记忆性


