本节笔记参考自：《人工智能：现代方法第4版》。

什么是智能体 (Agent)?

在书上有如下定义：任何通过传感器（sensor）感知环境（environment）并通过执行器（actuator）作用于该环境的事物都可以被视为智能体（agent）。

对人类来说，我们的眼睛和耳朵就是传感器；对机器人来说，它的红外探测器就可以看作是传感器。而环境是一个笼统的概念，我们所感知的周围的一切都可以看作环境，甚至整个宇宙。当然，实际问题中我们设计智能体中，所谓环境只关心智能体感知并且影响智能体动作的部分。关系如图所示。

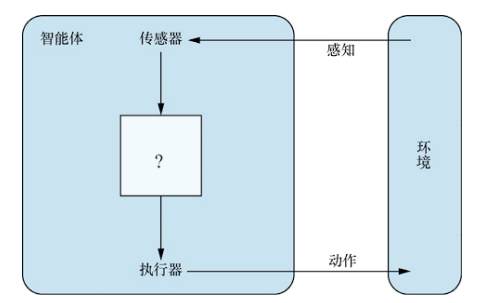
术语感知（percept 名词）表示智能体的传感器正在感知的内容。感知序列（percept sequence）表示智能体所感知的一切完整历史。那么一个智能体如何作出动作选择呢？一般来说是根据它的内置知识以及目前为止整个感知序列。数学上讲，我们说智能体的行为由智能体函数（agent function）描述，这个函数的作用是：完成一个感知序列→动作的映射。

做着正确事情的智能体叫理性智能体（rational agent）。对于智能体表现的评价由性能度量（performance measure）描述。性能度量评估智能体在环境中的行为。给定到目前为止所看到的感知序列，理性智能体的动作是为了最大化性能度量的期望值。

（后续接着补）

强化学习概述

强化学习（reinforcement learning）是一种无监督学习，智能体与世界进行互动并定期收到反映其表现的奖励（reward）。

我们考虑下国际象棋的问题。如果采用监督学习，那么我们要训练出一个模型：(当前局面)=下一步下棋走法。很容易想到，这样的数据集太过庞大了，不太可能实现；而且智能体很可能不知道最终的目标是什么，只是被训练的数据牵着鼻子走。因此我们需要强化学习——在这个例子中，我们可以设定获胜的奖励为1，失败的奖励为0，平局的奖励为1/2。对于“奖励”这一概念，先引出马尔科夫决策过程（MDP）。（目前都是概述）

马尔科夫决策过程

转移模型

转移模型是指给定先前状态值时，最新状态变量的概率分布，即：。现在我们面临一个问题：当t不断增长，条件集合会无限变大。解决这个问题的方式是马尔科夫假设（Markov assumption）：当前状态只依赖于有限固定数量的过去状态。对于满足这一假设的过程我们称之为马尔科夫过程（Markov process）或者马尔科夫链（Markov chain）。其中最简单的是一阶马尔科夫过程，即当前状态只依赖于前一个状态，即：。等式右侧的条件分布就是一阶马尔科夫过程的转移模型。结构如图。

序贯决策问题

在这种问题中，智能体的效用取决于一系列决策。转移模型描述了每个状态下每个动作的结果，这些结果是有随机性的，我们写作, 表示在状态s中执行动作a，达到状态s'的概率（也写作）。我们假设转移是马尔科夫的：从s到s'的概率只取决于s，而不取决于之前的状态。

我们规定对于通过动作a从s到s'的每次转移，智能体都会收到一个奖励。奖励可以正也可以负。在一个完全可观测的随机环境下，具有马尔科夫转移模型和加性奖励的序贯决策问题称为马尔科夫决策过程（Markov decision process）。动态规划是求解MDP的常用办法。

策略

MDP问题的解是什么样子的？没有固定的动作序列可以求解这个问题，因为智能体可能会以一种与目标不同的状态结束。因此问题的解必须告诉智能体在任何可能的状态下应该作什么动作。这种解称为策略，通常用来表示一个策略，用来表示策略对状态s推荐的动作。

最优策略（optimal policy）是指能够产生最大期望效用的策略，用表示。

从奖励中学习

先前我们在MDP中提到了奖励的概念，而事实上强化学习的目标也是相同的:最大化期望奖励总和。在强化学习中，智能体本身处于MDP里，它可能不知道转移模型或者奖励函数，必须采取行动以了解更多的信息。只要为智能体提供正确的奖励信号，强化学习就能提供一种非常通用的构建人工智能系统的方法。

强化学习可以根据方法的不同如下分类。

基于模型的强化学习

这些方法中，智能体使用环境的转移模型来帮助解释奖励信号并决定如何行动。模型可能最开始未知，智能体通过观测它的行为带来的影响来学习模型；也可能是已知的。基于模型的强化学习系统通常会学习一个效用函数,，它定义为状态s之后的奖励的综合。

无模型强化学习

这种方法中，智能体不知道环境的转移模型也不会学习这个模型。它会直接学习如何采取行为方式。主要有以下两种形式：

动作效用函数学习

动作效用函数（action-utility function），也称Q函数（Q-function）：是给定状态下采取给定动作a的期望效用，其与效用有关： .Q函数代表了从状态s出发，采取动作a的奖励的总和；智能体通过寻找具有最高Q值的动作来决定在状态s下采取的行动。

策略搜索

智能体学习一个策略,即从状态到动作的直接映射。

多智能体环境

很多时候一个智能体必须在包含多个行动者的环境中作出决策，这样的环境称之为多智能体系统（multiagent system）。在这种系统中，智能体要解决多智能体规划问题，其合适的解决方法取决于环境中各智能体间的关系。

上文中我们对强化学习做了一些概述，但都只是对于单智能体而言。下面主要介绍多智能体。By the way，多智能体强化学习的学习需要有博弈论的相关知识。从决策者的角度，多智能体系统分为单决策者和多决策者。

单决策者

我们考虑环境里有多个行动者，但只有一个决策者。此时，决策者告诉其他智能体该做什么。我们假设“智能体会简单地执行被告知的事情”——这个假设称作仁者假设（benevolent agent assumption）。但是即便在仁者假设下，多个行动者的行动也要考虑同步关系。对行动者A和B，他们可能会同时行动，也可能同一时刻某动作必须互斥，也可能必须满足某种先后关系（序贯动作）。

当然，如果每个主体的信息都能集中起来，然后给总体规划进行执行，那么一个多体问题也可以看作一个单智能体问题。当这种集中是无法实现时，我们就面临分散规划（decentralized planning）问题。

多决策者

不同于单决策者情况——试想我们环境中其他行动者也是决策者，它们中每一个都有着自己的偏好，都会自己规划、自己选择。我们称之为对应体（counterpart）。此时可分为两个情况：

1.虽然有多个决策者，但是共同目标是相同的。此时的问题主要是协调问题（coordination problem）：每个人都要朝着一个方向努力，不能彼此破坏规划。

2.每个决策者都有自己的偏好，即使这些偏好截然相反。

显然，这就意味着我们要进入博弈论的领域了。博弈论是多智能体系统决策的理论基础。博弈论可以通过两种方式用于人工智能：

1.智能体设计。智能体用博弈论分析可能的决策，假设其他智能体采取理性行动时计算每个决策的期望效用。

2.机制设计。我们可以定义环境规则，即智能体必须参与的博弈，使得每个智能体都采用自身效用最好的方案时，最大化集体利益。

博弈论为我们提供了一系列不同的模型，其中每个模型都有自己的一套基本假设。其中最重要的区别在于我们是否应该将其视为合作博弈。博弈分两种：

· 合作博弈。智能体之间存在一个具有约束力的协约，保证智能体之间稳健合作。

· 非合作博弈。非合作并不是说只有竞争没有合作。它只是说，没有中心协约来约束所有智能体合作，智能体可以自行决定合作，只要最大化自己利益就行。