多智能体学习参考了多智能体强化学习入门(六)——MFMARL算法(Mean
Field Multi-Agent RL) - 知乎
(zhihu.com)系列专栏,但是感觉很难懂。。此外,找到了一篇关于MARL领域概述的论文:
[2011.00583] An Overview
of Multi-Agent Reinforcement Learning from Game Theoretical Perspective
(arxiv.org)
论文一百多页,都写成教科书了。。慢慢看吧。
目前主要是对MF-MARL论文的阅读:1802.05438v4.pdf
(arxiv.org)。这是一篇比较新的论文,它应用了平均场的思想,当智能体规模庞大,维度变得巨大的时候,它将智能体群体的相互作用近似为中心智能体和邻居的近似作用;文章的证明写的比较迷,但是论文给的实验数据证明了MF-Q和MF-AC胜过独立Q-learning以及它们在大规模多智能体下的性能。
同时,对于代码也在逐行理解阅读(结合pdb库不断调试)。目前对于论文的理解见下(收敛性的证明太难了看不懂。。另外很想吐槽这论文向量有时候加粗有时候不加粗太过分了):
首先,论文指出目前的MARL方法有数量限制,当智能体数量增加时,由于维度灾难和智能体交互的指数级增长,学习非常困难。因此本文提出平均场强化学习MFRL(Mean
Field RL),把智能体群体的交互近似为中心智能体 和
邻居智能体(或者整个群体,本顺便一提文的代码好像是这么写的)的平均作用
的交互。两个实体的相互作用是相互加强的(没说why?);文章提出了MF-Q和MF-AC,并且在gaussian
squeeze(我甚至搜不到这是啥)、Ising
model(就是平均场物理模型)和Magent进行了实验。当然前两个不用看,我们的重心是Magent的代码。
传统的算法有独立Q学习,这是把其他智能体看作环境,让单个智能体和环境交互。理论上,这会失败,因为不具有收敛性,一个智能体的策略的改变会影响其他人的策略。研究表明,在许多场景下,了解联合行动效果的智能体比不了解的具有更好的性能,在实践中呢也确实很多情况下需要大量代理之间的策略交互(如MMO),但是直接求解纳什均衡具有极高的复杂性。因此本文提出了平均场RL(在平均场思想下,通过一系列智能体相互作用,任何一对智能体是可以全局连接的)。
在开始MF之前,我们要给出几个初步的式子。 这个式子表明了在联结策略(joint
policy)下,智能体j在状态s下的值函数。这个和单智体的定义差不多。然后,在联结动作下,智能体在联结策略下的Q函数就可以写成:
那根据单智体的知识显然v和q就有如下等式:
这里要指出,我们根据离散时间下的非合作设置下的随机博弈来指定MARL,并不考虑明确的联盟;每个智能体不知道别人的奖励函数,但是能够观察其他智能体之前的动作以及由动作得到的奖励。MARL中,智能体的目标就是得到纳什均衡下的最优策略以最大化其Q值,所谓纳什均衡就是任一智能体都不可能只改变自身策略而获得更大的v值:
这里的-j就是表示除了自己的意思(这种表示法叫做compact
notation,紧凑表示法):。给定一个纳什策略π,纳什Q值就是:。注意这玩意是个向量。
联合行动的维度随着智能体数量N成比例增长,所有智能体根据联合行动评估Q值,因此学习标准Q函数不可行。为此,论文使用成对的局部作用分解Q值:
这里的N^j是邻居数量。值得指出,智能体与邻居们的成对估计降低了复杂度,又保留了全局交互。在这个方程中,成对交互可以用平均场理论估计(注意到此才有MF思想)。我们考虑离散动作空间,对j的采取的动作,我们可以采取one-hot编码,比如四维离散空间采取动作3就表示为:[0,0,1,0]。也就是说,这里的a是个向量:。我们可以计算出j的邻居们的平均动作(注意是平均,不是-j!论文也提到,这个平均动作看作是一个动作分布),然后以此表示出j每个邻居k的one-hot编码动作:
就是说,比如俩智能体,一个动作[0,0,1],一个动作[0,1,0],那么平均动作就是[0,0.5,0.5]。而是一个小幅波动,你想嘛邻居和邻居们的平均值之间肯定有一个差的。在代码里,求平均代码是这么写的:

根据泰勒展开,我们可以得到: 注意这里(这些波动误差肯定就彼此抵消了)。这样,两两成对的智能体的相互作用就被建模成了,一个中心实际智能体和周围邻居平均出来的虚拟智能体的相互作用。论文给出如下示意图:
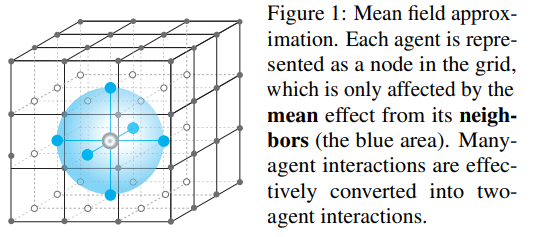
给定我们的经验为:,如同单智体的QL,我们的更新公式为:
与单智体类似。这里的平均场值函数定义为: 这样就可以算策略了。在阶段博弈{},首先依据当前策略算出每个,然后当前策略由于依赖发生了变化,我们用玻尔兹曼策略公式修改:
这就是单智体一样的,平衡探索与利用用的。代码中的ValueNet有个temperature,就是控制这玩意的(应该吧),越高越探索。通过不断这样迭代,所有智能体的平均动作和相应策略π交替改进,最终收敛(收敛的部分暂时看不懂!!这部分证明超出本科范围了。。)。然后呢为了和方程10的MF
value function分开,作者用平均场算子的形式表示了:
实际上这个算子形成了一个收缩映射(证明略。什么是收缩映射?参考:强化学习(三):贝尔曼最优方程(BOE)
| 雨白的博客小屋 (ameshiro77.cn)),这样就会让MF Q最终收敛到Nash
Q。
我们对于off-policy方法可以利用标准QL或DPG(这也说明ML可以应用到DDPG?把策略神经网络输出取平均应该更容易;另外PPO也有off版本的,应该也能应用?),我们可以改造成MF
-Q。损失函数为: 其中,是MF
Value的目标值。求导就是: (那个是L。)在MF-AC中,策略梯度也和单智体差不多,长这样:
那个是F。,,都是神经网络的参数。MF-AC的critic与MF-Q同设置(依据方程(4))。
收敛部分太难了目前看不懂,算法如下:

是QL更新目标网络时选取软更新方法的参数。硬更新可能不太稳定。




