​ 本周报主要为RL学习笔记以及一些配合学习的代码实现。首先是RL的学习路线：

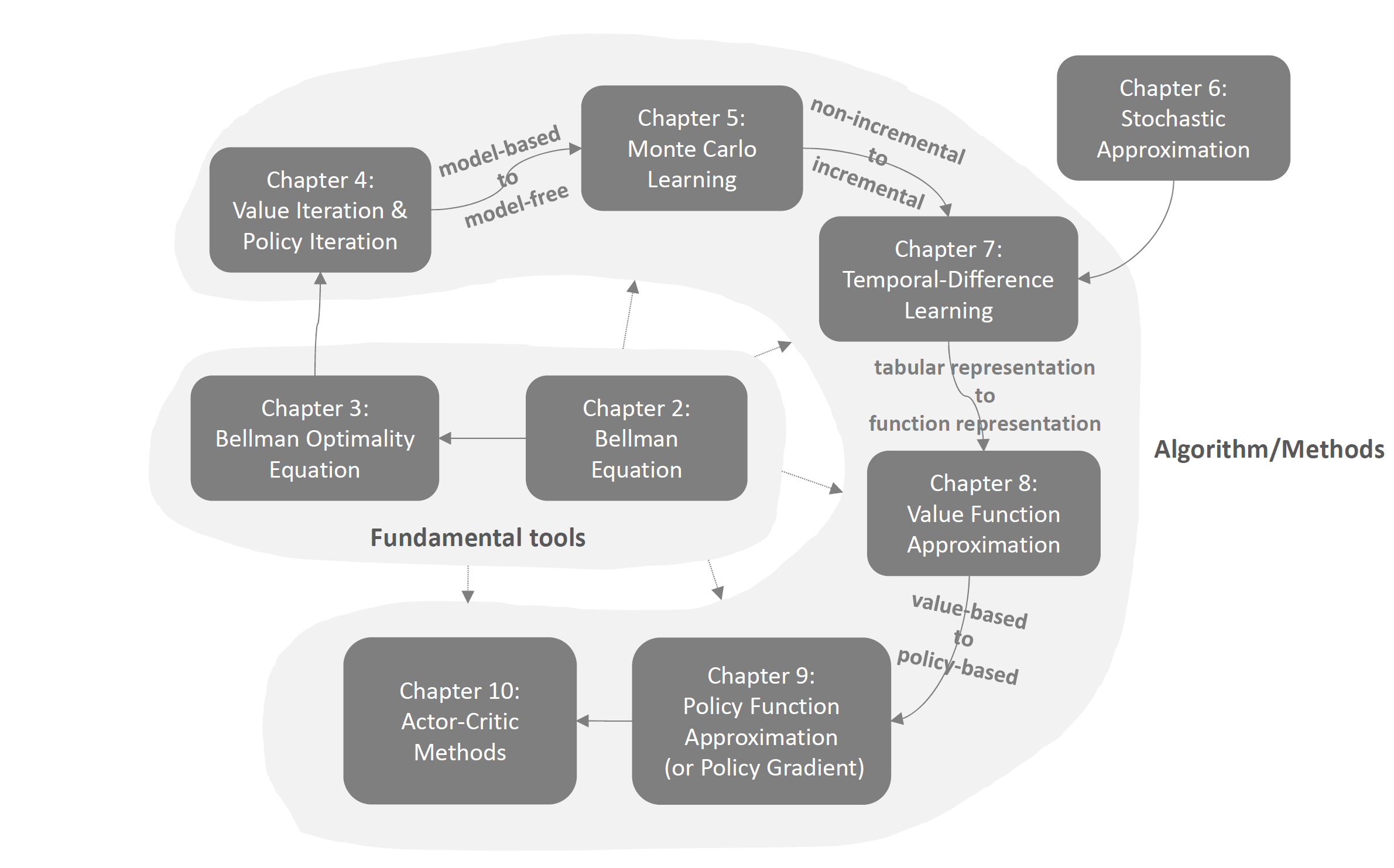
Figure_chapterRelationship

​ 首先是学习基本概念以及基本工具：贝尔曼方程和贝尔曼最优方程。在此之上，我们学习基于model的值迭代、策略迭代方法。 然后我们学习mode-free的蒙特卡洛学习。之后是时间差分学习，并从此出发从tabular representation过渡到function representation，此时神经网络就会进入强化学习，我们会学到著名的DQN。再之后就是从value-based过渡到policy-based，学习策略梯度下降。最后便是actor critic算法，集合了许多东西，之后就可以去看多智能体了。

​ 在本周报中，主要内容是写完了基本概念的完整介绍和贝尔曼方程的详细推导，详见：

强化学习(一):基本概念 | 雨白的博客小屋 (ameshiro77.cn)

强化学习(二):贝尔曼方程 | 雨白的博客小屋 (ameshiro77.cn)

​ 在贝尔曼方程的基础上，参考一些博客实现了简单的代码。背景是一个网格世界，如下：

image-20230715132925774

​ 除了头尾终点，其他地方的reward均为-1。代码求解state value如下。

​ 首先是一些关于env，action，state，reward之类的定义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np

import copy

TOTAL_ROWS = 4

TOTAL_COLUMN = 4

TOTAL_ACTIONS_NUM = 4  # 0代表上，1代表右，2代表下，3代表左

STOP_CRITERION = 1e-4

GAMMA = 1

REWARD_SETTING = -1

ACTION_DICT = {0: '上', 1: '右', 2: '下', 3: '左'}

FOUR_ACTION_PROBABILITY = {'上': 0.25, '右': 0.25, '下': 0.25, '左': 0.25}  # 分别是走上、下、左、右的概率。

IDX_CHANGE_DICT = {'上': (-1, 0), '右': (0, 1), '下': (1, 0), '左': (0, -1)}  # 左边这个是行的索引的改变，右边这个是列的索引的改变

​ 然后定义一个函数，返回采取行动后得到的奖励和到达的状态。我们的例子比较简单，除了可以选择不同action外，都是deterministic case。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def get_current_reward_and_next_state(current_state, action):
    #根据当前的状态，以及行为，计算当前行为的奖励以及下一个状态
    # =====
    # 如果是在终点，原地转圈 奖励为0
    row_idx, column_idx = current_state
    if (row_idx == 0 and column_idx == 0):
        return 0, (0, 0)

    if (row_idx == 3 and column_idx == 3):
        return 0, (3, 3)

    # =====
    # 否则:根据传入的行动，计算移动后的位置
    next_row_idx = row_idx + IDX_CHANGE_DICT[action][0]
    next_column_idx = column_idx + IDX_CHANGE_DICT[action][1]
    # 如果移动到边缘就原地不动，否则就移动，奖励固定
    if next_row_idx < 0 or next_row_idx > TOTAL_ROWS - 1 or next_column_idx < 0 or next_column_idx > TOTAL_COLUMN - 1:
        return REWARD_SETTING, (row_idx, column_idx)
    else:
        return REWARD_SETTING, (next_row_idx, next_column_idx)

​ 之后定义每一个状态初始的state value为0，用一个矩阵表示：

1
V = np.zeros((TOTAL_ROWS, TOTAL_COLUMN))

​ 然后就可以开始迭代更新state-value了。如果使用直接计算的话，计算代价非常高，因此我们选择使用迭代的方法求解，方法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 开始迭代更新状态价值函数
iteration = 0
flag = True
while flag:
    delta = 0
    old_V = copy.deepcopy(V)
    # 遍历每一个状态，对其进行更新
    for row_idx in range(TOTAL_ROWS):
        for column_idx in range(TOTAL_COLUMN):
            new_final_value = 0
            for each_action in range(TOTAL_ACTIONS_NUM):
                action = ACTION_DICT[each_action]
                action_proba = FOUR_ACTION_PROBABILITY[action]
                current_action_reward, next_state = get_current_reward_and_next_state((row_idx, column_idx), action)
                new_final_value = new_final_value + action_proba * (1 * (current_action_reward + GAMMA * V[next_state[0]][next_state[1]]))
            V[row_idx][column_idx] = new_final_value
    delta = max(delta, abs(old_V - V).max())
    if delta < STOP_CRITERION:
        flag = False
    iteration += 1

​ 其中最关键的就是这句代码：

1
new_final_value = new_final_value + action_proba * (1 * (current_action_reward + GAMMA * V[next_state[0]][next_state[1]]))

​ 它就对应着我们贝尔曼方程： ​ 因为我们的例子里除了π都是离散的，所以中间的概率都是1.最后得到的state value表为：

image-20230715134003870

​ 假设我们在状态7，那我们沿着四周state-value最大的地方走，就可以得到路径为7-6-5-0. 这就是最简单的强化学习。

​ openai gym方面，跑了几个简单的例子，也大致知道了在gym里env的作用以及一些函数和返回值。不过用的都是很传统的方法比如Q-learning，还没有加入神经网络。（数学部分学到后面再说）

​ 下周安排：看完贝尔曼最优方程和蒙特卡洛（也就是看完cp.5），然后去看看NMMO2.0的最新官网，进虚拟机自定义地改改他们的代码试试，做一个代码方面启发式的探索。（以及还要复习408笔试，顺便看一点计算机图形学+Unity...）