论文地址：[2403.03545] Diffusion-based Generative Prior for Low-Complexity MIMO Channel Estimation (arxiv.org)

摘要

本文提出了一种基于DM（diffusion model）的信道估计器。相比其他的使用先验生成器的工作，该工作设计了一种“轻量级的，带有SNR信息的位置编码”的CNN，并在稀疏角域（sparse angular domain）学习。本文的估计策略避免了随机重采样，截断那些SNR低于给定导频观测值的逆向扩散步骤，使得估计器复杂度低且内存开销很小。

简介

生成模型可以学习复杂的数据分布，并且可以利用这一先验知识在无线通信上。DM和一些基于score的模型生成能力很强，但有非常大的计算开销（比如逆向过程中每一步都要用大型NN重采样），不能用到像信道估计这样的实时应用中。

近期有工作（[2403.02957] On the Asymptotic Mean Square Error Optimality of Diffusion Models (arxiv.org)）提出一种判别式去噪策略（deterministic denoising strategy），其中观测的SNR 程度与对应DM的时间步相关；这种策略大幅度减少了逆向步骤，无需重采样。更进一步，这种去噪策略在扩散时间步很多时是渐进均方差最优（asymptotically mean square error(MSE)）的。对于实际分布，不多的时间步就可以让去噪性能接近条件均值估计器（conditional mean estimator , CME）。然而因为应用了百万级参数的复杂架构，这些方法还是不能实际用到像MIMO这样的信道估计中。本文针对MIMO信道，考虑到其结构特性（即在角域/波束空间域的稀疏性，英文sparsity in the angular/beamspace domain），可以设计参数更少的轻量级NN。

CME参考：《Fundamentals of Wireless Communication》的Appendix3 ，地址：https://web.stanford.edu/~dntse/papers/book121004.pdf。

本文的主要贡献为：1.提出一个将现有顶级DM作为先验生成器的信道估计器；2.为了降低复杂度和开销，用轻量CNN设计信道估计器，在稀疏角域学习信道分布；3.获得了更好的性能；4.强调了本文信道估计器与MSE最优的CME的联系，以及其渐进最优。

前置知识

MIMO系统建模

考虑上行传输：一个配有的移动终端向配有的基站（BS）发送个导频，接收到的信号定义为（是复数域）：其中，是未知分布下的无线信道矩阵，是接收器可知的导频矩阵，是有列的AWGN，服从高斯分布，方差为。本文考虑，即导频观测是完全的，且导频矩阵是酉矩阵（unitary pilot matrix），即一个DFT矩阵，满足（是矩阵的共轭转置，即先共轭再转置）。本文中，用小写粗体对矩阵进行向量化表示，即。通过在预处理过程中确保，可以定义SNR为（在上述AMSE论文中提及）。

扩散模型

基本扩散模型公式就不赘述了。文章指出，DM时间步可以等价地解释为不同的SNR步，通过定义DM在t时刻的SNR为：显然，随着t增加，SNR逐渐减小（噪声越来越大）。

信道估计

MSE形式的最优信道估计器是CME，定义为：该CME式子高度非线性，且如果先验分布未知，CME难以计算。因此，本文采用DM作为先验生成器去参数化一个隐式学习了先验分布的信道估计器。

基于DM的信道估计器

不同于图像等领域的自然信号，无线通信信道有独特的结构化属性。最为人所知的是，信道可以通过傅里叶变换变换到角域/波束空间域的表示形式。在大规模MIMO中，角域表示是非常稀疏、高度压缩的，尤其是在多径传播聚类数量（？）和角扩散（？）很低时，比如mmWave。因此，在角域训练DM学习信道分布的话，参数更少，速度更快更稳定。

不过我们还未对信道分布的稀疏级别或结构作出假设。因此，给定一个训练集，本文先把它转换到角域：，这一步可由二维FFT实现。之后，DM就正常地通过最大化ELBO离线训练。

对于在线信道估计，本文采用判别式逆向过程（即上述论文所述）并做出一些更改。首先，导频矩阵通过计算最小二乘解（least sqaure，LS）去相关（协方差矩阵化对角？），即：其中，是方差为的AWGN（由于P是酉矩阵）。假设知道观测的SNR，因为DM是方差不变的，因此LS估计被归一化为。之后，观测值通过FFT转变为角域，记作。需要指出，噪声不受傅里叶变换影响。之后，通过之前提到的DM中的SNR表示，我们可以找出DM最匹配观测值SNR的时间步：之后，DM的逆向过程通过设置来初始化。结果是：观测值的SNR越高，DM要执行的逆向过程就越少，信道估计的延迟就越低。这与一些工作中，在推理过程用iid的高斯噪声初始化且逆向采样过程完整的做法不同。

在初始化一个中间的DM时间步之后，式中逐时间步的条件均值从向t=1迭代，而无需从中抽取随机样本，最终得到估计。这可以定义为是一堆NN的拼接：最终估计再通过逆FFT回到空间域，得到。整体算法如图：

渐进最优

看不懂，主要就是说AMSE的工作能收敛于CME，然后因为FFT和导频去相关是可逆的，本文方法也是能收敛的。然后文章又说，假设BS收到的导频信号来自一个有限的SNR范围，本文用较少的DM步骤就能达到很好的效果。

网络架构

比起DDPM工作使用的复杂NN架构，本文设计了一个轻量的CNN。网络架构如下图所示：

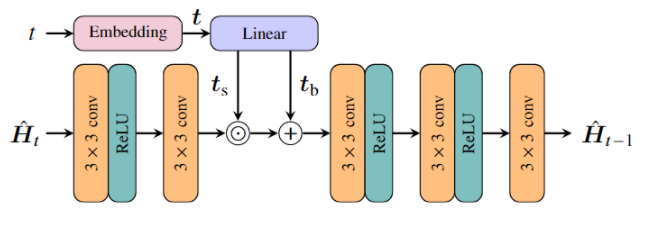
在全部DM时间步，参数共享。然后，Transformer中的正弦位置编码用来表示时间/SNR信息，记作，具体来说如图所示，在经过一个线性层后，分成一个scaling vector 和一个bias vector 。

网络中，先把输入的实部虚部stack到两个卷积通道中（3x3x2），然后卷积通道逐步增加到；之后再三个2D conv逐渐降低通道数。

实验结果

采用两种数据集 quadriga和3gpp。